insertion_procedure (int a[], int p [], int N)
{
int i,j,k;
for (i=0; i<=N; i++) p[i] = i;
for (i=2; i<=N; i++)
{
k = p[i];
j = 1;
while (a[p[j-1]] > a[k]) {p[j] = p[j-1]; j--}
p[j] = k;
}
}
Je dois trouver la complexité cyclomatique pour ce code et ensuite suggérer quelques cas de test en boîte blanche et des cas de test en boîte noire. Mais j'ai du mal à faire un CFG pour le code.Graphique de flux de contrôle et complexité cyclomatique pour la procédure suivante
J'apprécierais aussi de l'aide sur les cas de test.
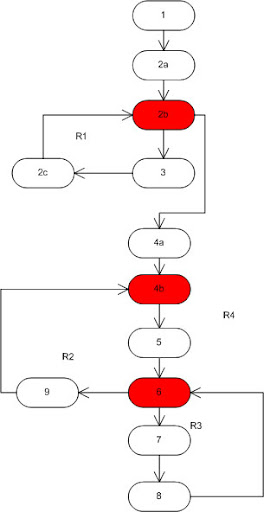
Quelle langue est-ce? Il ressemble à C sauf pour le "Int" plutôt que "int" dans la déclaration. Si c'est C, il n'y a pas de boucle for imbriquée, mais ratehr a une boucle while imbriquée dans une boucle for. –
Oh oui il n'y a pas de boucle imbriquée. Son C –