Pour l'un de mes projets de cours, j'ai commencé à implémenter un classificateur bayésien Naive en C. Mon projet consiste à implémenter une application classifieur de documents (en particulier Spam) en utilisant d'énormes données d'apprentissage.Problème avec l'opération de précision en virgule flottante en C
Maintenant, j'ai un problème pour implémenter l'algorithme en raison des limitations du type de données du C.
(algorithme J'utilise est donnée ici, http://en.wikipedia.org/wiki/Bayesian_spam_filtering)
PROBLÉMATIQUE: L'algorithme consiste à prendre chaque mot dans un document et calcul de la probabilité de celui-ci étant mot de spam. Si p1, p2 p3 .... pn sont des probabilités du mot-1, 2, 3 ... n. La probabilité de doc étant un spam ou non est calculée à l'aide

Ici, la valeur de probabilité peut être très facilement autour de 0,01. Donc, même si j'utilise le type de données "double", mon calcul ira pour un tirage au sort. Pour confirmer cela, j'ai écrit un exemple de code donné ci-dessous.
#define PROBABILITY_OF_UNLIKELY_SPAM_WORD (0.01)
#define PROBABILITY_OF_MOSTLY_SPAM_WORD (0.99)
int main()
{
int index;
long double numerator = 1.0;
long double denom1 = 1.0, denom2 = 1.0;
long double doc_spam_prob;
/* Simulating FEW unlikely spam words */
for(index = 0; index < 162; index++)
{
numerator = numerator*(long double)PROBABILITY_OF_UNLIKELY_SPAM_WORD;
denom2 = denom2*(long double)PROBABILITY_OF_UNLIKELY_SPAM_WORD;
denom1 = denom1*(long double)(1 - PROBABILITY_OF_UNLIKELY_SPAM_WORD);
}
/* Simulating lot of mostly definite spam words */
for (index = 0; index < 1000; index++)
{
numerator = numerator*(long double)PROBABILITY_OF_MOSTLY_SPAM_WORD;
denom2 = denom2*(long double)PROBABILITY_OF_MOSTLY_SPAM_WORD;
denom1 = denom1*(long double)(1- PROBABILITY_OF_MOSTLY_SPAM_WORD);
}
doc_spam_prob= (numerator/(denom1+denom2));
return 0;
}
J'ai essayé Float, double et même long double types de données, mais toujours le même problème. Donc, disons dans un document de 100K mots que j'analyse, si seulement 162 mots ont 1% de probabilité de spam et que 99838 sont des mots de spam, alors mon application le dira comme non Spam doc à cause de l'erreur Precision (comme le numérateur va facilement à ZERO) !!!
C'est la première fois que je suis confronté à ce problème. Alors, comment exactement ce problème devrait être abordé?

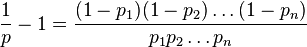



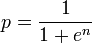
+1. J'ai mis à jour ma réponse. Je pense que le mieux est de combiner les deux algorithmes, puisque le mien subit moins de perte de précision pour le calcul des facteurs, et le vôtre moins pour le calcul du produit global. – back2dos