Je suis en train de programmer un jeu et je suis arrivé à un point très difficile. Fondamentalement, j'ai un cercle et j'ai 2 angles sur ce cercle. L'angle 1 (A) est un point vers lequel je veux que l'angle 2 (B) passe. Au cours de mon jeu chaque cadre que j'ai besoin de vérifier ou non pour augmenter ou diminuer ma valeur d'angle d'une certaine quantité (vitesse) pour finalement atteindre le premier angle. Ma question est comment je fais ça?Comment savoir quand augmenter ou diminuer l'angle pour obtenir un angle spécifique?
J'ai essayé de le faire mais je ne semble pas le faire correctement.
bool increase = false;
float B = [self radiansToDegrees:tankAngle];
float A = [self radiansToDegrees:tankDestinationAngle];
float newAngle = B;
if(B < A) {
float C = B - (360 - A);
float D = A - B;
if(C < D) increase = false;
else increase = true;
} else if(B > A) {
float C = B - A;
float D = A - (360 - B);
if(C < D) increase = false;
else increase = true;
}
if(increase) {
newAngle += 1.0;
} else {
newAngle -= 1.0;
}
if(newAngle > 360.0) {
newAngle = 0 + (newAngle - 360.0);
} else if(newAngle < 0.0) {
newAngle = 360 + newAngle;
}
if(newAngle == 0) newAngle = 360;
newAngle = [self degreesToRadians:newAngle];
[self setTanksProperPositionRotation:newAngle];
L'effet de base que je suis en train de réaliser est lorsque l'utilisateur fait un nouveau point, ce qui serait l'angle 1, l'angle 2 se déplacerait vers l'angle 1 choisir la direction la plus rapide. Je pense que j'ai passé environ 4 heures à essayer de comprendre cela.

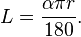
Merci beaucoup. J'ai juste compris ce que signifie le premier symbole de l'équation. – Thomas
@ Thomas: Je suis content que je puisse aider. Voulez-vous dire le 'a'? C'est l'angle mesuré en degrés. Si vous avez l'angle en radians alors le type est plus simple: 'L = theta * r' –
Cette réponse est inutile. Puisque r, pi et 180 sont toutes des constantes, vous dites en gros * "utilisez l'angle le plus petit" * - c'est ce qui le dérange! –