Ajout successif de char pour obtenir le mot le plus long du dictionnaire

Question

Étant donné un dictionnaire de mots et un caractère initial. trouver le mot le plus long possible dans le dictionnaire en ajoutant successivement un caractère au mot. À n'importe quel exemple, le mot devrait être un mot valide dans le dictionnaire.

ex: a -> à -> cat -> panier -> Tableau ....

Answer 1

L'approche de la force brute serait d'essayer d'ajouter des lettres à chaque index disponibles à l'aide d'une recherche en profondeur d'abord. Donc, en commençant par 'a', il y a deux endroits où vous pouvez ajouter une nouvelle lettre. Devant ou derrière le 'a', représenté par des points ci-dessous.

.a.

Si vous ajoutez un 't', il y a maintenant trois positions.

.a.t.

Vous pouvez essayer d'ajouter à chaque position disponible toutes les 26 lettres. Le dictionnaire dans ce cas peut être une simple hashtable. Si vous ajoutez un 'z' au milieu, vous obtenez 'azt' qui ne serait pas dans la hashtable donc vous ne continuez pas ce chemin dans la recherche.

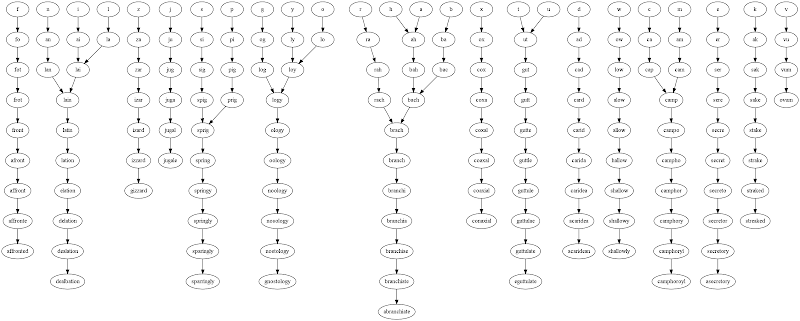
Édition: Le graphique de Nick Johnson m'a rendu curieux de savoir à quoi ressemblerait un graphique de tous les chemins maximaux. Il est un grand (1,6 Mo) l'image ici:

http://www.michaelfogleman.com/static/images/word_graph.png

Modifier: Voici une implémentation de Python. L'approche par force brute fonctionne réellement dans un laps de temps raisonnable (quelques secondes, selon la lettre de départ).

import heapq 

letters = 'abcdefghijklmnopqrstuvwxyz' 

def search(words, word, path): 
    path.append(word) 
    yield tuple(path) 
    for i in xrange(len(word)+1): 
     before, after = word[:i], word[i:] 
     for c in letters: 
      new_word = '%s%s%s' % (before, c, after) 
      if new_word in words: 
       for new_path in search(words, new_word, path): 
        yield new_path 
    path.pop() 

def load(path): 
    result = set() 
    with open(path, 'r') as f: 
     for line in f: 
      word = line.lower().strip() 
      result.add(word) 
    return result 

def find_top(paths, n): 
    gen = ((len(x), x) for x in paths) 
    return heapq.nlargest(n, gen) 

if __name__ == '__main__': 
    words = load('TWL06.txt') 
    gen = search(words, 'b', []) 
    top = find_top(gen, 10) 
    for path in top: 
     print path 

Bien sûr, il y aura beaucoup de liens dans la réponse. Ceci imprimera les N premiers résultats, mesurés par la longueur du mot final.

Sortie pour la lettre de début 'a', en utilisant le dictionnaire TWL06 Scrabble.

(10, ('a', 'ta', 'tap', 'tape', 'taped', 'tamped', 'stamped', 'stampede', 'stampedes', 'stampeders')) 
(10, ('a', 'ta', 'tap', 'tape', 'taped', 'tamped', 'stamped', 'stampede', 'stampeder', 'stampeders')) 
(10, ('a', 'ta', 'tan', 'tang', 'stang', 'strang', 'strange', 'strangle', 'strangles', 'stranglers')) 
(10, ('a', 'ta', 'tan', 'tang', 'stang', 'strang', 'strange', 'strangle', 'strangler', 'stranglers')) 
(10, ('a', 'ta', 'tan', 'tang', 'stang', 'strang', 'strange', 'stranges', 'strangles', 'stranglers')) 
(10, ('a', 'ta', 'tan', 'tang', 'stang', 'strang', 'strange', 'stranges', 'strangers', 'stranglers')) 
(10, ('a', 'ta', 'tan', 'tang', 'stang', 'strang', 'strange', 'stranges', 'strangers', 'estrangers')) 
(10, ('a', 'ta', 'tan', 'tang', 'stang', 'strang', 'strange', 'stranges', 'estranges', 'estrangers')) 
(10, ('a', 'ta', 'tan', 'tang', 'stang', 'strang', 'strange', 'stranger', 'strangler', 'stranglers')) 
(10, ('a', 'ta', 'tan', 'tang', 'stang', 'strang', 'strange', 'stranger', 'strangers', 'stranglers')) 

Et voici les résultats pour chaque lettre de départ. Bien sûr, une exception est faite que la lettre de début unique ne doit pas être dans le dictionnaire. Juste un mot de 2 lettres qui peut être formé avec.

(10, ('a', 'ta', 'tap', 'tape', 'taped', 'tamped', 'stamped', 'stampede', 'stampedes', 'stampeders')) 
(9, ('b', 'bo', 'bos', 'bods', 'bodes', 'bodies', 'boodies', 'bloodies', 'bloodiest')) 
(1, ('c',)) 
(10, ('d', 'od', 'cod', 'coed', 'coped', 'comped', 'compted', 'competed', 'completed', 'complected')) 
(10, ('e', 're', 'rue', 'ruse', 'ruses', 'rouses', 'arouses', 'carouses', 'carousels', 'carrousels')) 
(9, ('f', 'fe', 'foe', 'fore', 'forge', 'forges', 'forgoes', 'forgoers', 'foregoers')) 
(10, ('g', 'ag', 'tag', 'tang', 'stang', 'strang', 'strange', 'strangle', 'strangles', 'stranglers')) 
(9, ('h', 'sh', 'she', 'shes', 'ashes', 'sashes', 'slashes', 'splashes', 'splashers')) 
(11, ('i', 'pi', 'pin', 'ping', 'oping', 'coping', 'comping', 'compting', 'competing', 'completing', 'complecting')) 
(7, ('j', 'jo', 'joy', 'joky', 'jokey', 'jockey', 'jockeys')) 
(9, ('k', 'ki', 'kin', 'akin', 'takin', 'takins', 'takings', 'talkings', 'stalkings')) 
(10, ('l', 'la', 'las', 'lass', 'lassi', 'lassis', 'lassies', 'glassies', 'glassines', 'glassiness')) 
(10, ('m', 'ma', 'mas', 'mars', 'maras', 'madras', 'madrasa', 'madrassa', 'madrassas', 'madrassahs')) 
(11, ('n', 'in', 'pin', 'ping', 'oping', 'coping', 'comping', 'compting', 'competing', 'completing', 'complecting')) 
(10, ('o', 'os', 'ose', 'rose', 'rouse', 'rouses', 'arouses', 'carouses', 'carousels', 'carrousels')) 
(11, ('p', 'pi', 'pin', 'ping', 'oping', 'coping', 'comping', 'compting', 'competing', 'completing', 'complecting')) 
(3, ('q', 'qi', 'qis')) 
(10, ('r', 're', 'rue', 'ruse', 'ruses', 'rouses', 'arouses', 'carouses', 'carousels', 'carrousels')) 
(10, ('s', 'us', 'use', 'uses', 'ruses', 'rouses', 'arouses', 'carouses', 'carousels', 'carrousels')) 
(10, ('t', 'ti', 'tin', 'ting', 'sting', 'sating', 'stating', 'estating', 'restating', 'restarting')) 
(10, ('u', 'us', 'use', 'uses', 'ruses', 'rouses', 'arouses', 'carouses', 'carousels', 'carrousels')) 
(1, ('v',)) 
(9, ('w', 'we', 'wae', 'wake', 'wakes', 'wackes', 'wackest', 'wackiest', 'whackiest')) 
(8, ('x', 'ax', 'max', 'maxi', 'maxim', 'maxima', 'maximal', 'maximals')) 
(8, ('y', 'ye', 'tye', 'stye', 'styed', 'stayed', 'strayed', 'estrayed')) 
(8, ('z', 'za', 'zoa', 'zona', 'zonae', 'zonate', 'zonated', 'ozonated')) 

Answer 2

Si vous voulez faire une fois, je ferais ce qui suit (généralisé au problème de commencer par un mot complet):

Prenez tout votre dictionnaire et jeter tout ce qui n'a pas un surensemble des caractères dans votre mot cible (disons qu'il a la longueur m). Puis bin les mots restants par longueur. Pour chaque mot de longueur m+1, essayez de laisser tomber chaque lettre et voir si cela donne le mot désiré. Sinon, jetez-le. Ensuite, vérifiez chaque mot de longueur m+2 par rapport à l'ensemble valide de longueur m+1, en supprimant tout ce qui ne peut pas être réduit. Continuez jusqu'à ce que vous trouviez un ensemble vide; la dernière chose que vous avez trouvée sera la plus longue.

Si vous voulez que ceci soit rapide pour rechercher, je construirais un suffix-arbre-comme structure de données.

Groupez tous les mots par longueur. Pour chaque mot de longueur 2, placez chacun de ses deux caractères dans un ensemble "subword", et ajoutez ce mot à chacun des ensembles "superword" des caractères. Maintenant, vous avez un lien entre tous les mots valides de longueur 2 et tous les caractères. Faites de même avec des mots de longueur 3 et des mots valides de longueur 2. Vous pouvez maintenant commencer n'importe où dans cette hiérarchie et faire une recherche de grande envergure pour trouver la branche la plus profonde.

---

Edit: la vitesse de cette solution dépendra en grande partie de la structure de la langue, mais si nous décidons de construire tout en utilisant des jeux avec log(n) performances pour toutes les opérations (par exemple nous utilisons des arbres rouge-noir ou similaire), et nous avons N(m) mots de longueur m, puis pour former le lien entre les mots de longueur m+1 et m sera environ (m+1)*m*N(m+1)*log(N(m)) temps (en tenant compte que la chaîne compare prendre temps linéaire dans la longueur de la chaîne). Puisque nous devons le faire pour toutes les longueurs de mot, le moteur d'exécution pour la construction de la structure de données complète sera quelque chose de l'ordre de

(typical word length)^3 * (dictionary length) * log (dictionary length/word length) 

(Le binning initial en mots d'une certaine longueur prendra du temps linéaire ne peut donc être négligé: la formule d'exécution est compliquée car elle dépend de la distribution des longueurs de mots: dans le cas où vous le faites depuis un seul mot, c'est encore plus compliqué car cela dépend du nombre attendu de mots plus longs avec des sous-mots plus courts .)

Answer 3

en supposant que vous devez faire cela à plusieurs reprises (ou si vous voulez la réponse pour chacun des 26 lettres), faites-le à l'envers:

1. charge un dictionnaire et le tri par longueur, descendant
2. établir la cartographie, initialement vide, entre les mots et (extension, max_len) tuples.
3. Pour chaque mot dans la liste triée:
   1. S'il est déjà dans la cartographie, récupérer le maximum len.
   2. Si ce n'est pas le cas, définissez la longueur maximale sur la longueur du mot.
   3. Examinez chaque mot produit en supprimant un caractère. Si ce mot n'est pas dans la cartographie, ou notre max_len dépasse le max_len du mot déjà dans la cartographie, mettez à jour la mise en correspondance avec le mot en cours et max_len

Ensuite, pour obtenir la chaîne pour une donnée préfixe, commencez simplement par ce préfixe et regardez-le à plusieurs reprises et ses extensions dans le dictionnaire.

est ici l'exemple de code Python:

words = [x.strip().lower() for x in open('/usr/share/dict/words')] 
words.sort(key=lambda x:len(x), reverse=True) 
word_map = {} # Maps words to (extension, max_len) tuples 

for word in words: 
    if word in word_map: 
    max_len = word_map[word][1] 
    else: 
    max_len = len(word) 
    for i in range(len(word)): 
    new_word = word[:i] + word[i+1:] 
    if new_word not in word_map or word_map[new_word][2] < max_len: 
     word_map[new_word] = (word, max_len) 

# Get a chain for each letter 
for term in "abcdefghijklmnopqrstuvwxyz": 
    chain = [term] 
    while term in word_map: 
    term = word_map[term][0] 
    chain.append(term) 
    print chain 

et sa sortie pour chaque lettre de l'alphabet:

['a', 'ah', 'bah', 'bach', 'brach', 'branch', 'branchi', 'branchia', 'branchiae', 'branchiate', 'abranchiate'] 
['b', 'ba', 'bac', 'bach', 'brach', 'branch', 'branchi', 'branchia', 'branchiae', 'branchiate', 'abranchiate'] 
['c', 'ca', 'cap', 'camp', 'campo', 'campho', 'camphor', 'camphory', 'camphoryl', 'camphoroyl'] 
['d', 'ad', 'cad', 'card', 'carid', 'carida', 'caridea', 'acaridea', 'acaridean'] 
['e', 'er', 'ser', 'sere', 'secre', 'secret', 'secreto', 'secretor', 'secretory', 'asecretory'] 
['f', 'fo', 'fot', 'frot', 'front', 'afront', 'affront', 'affronte', 'affronted'] 
['g', 'og', 'log', 'logy', 'ology', 'oology', 'noology', 'nosology', 'nostology', 'gnostology'] 
['h', 'ah', 'bah', 'bach', 'brach', 'branch', 'branchi', 'branchia', 'branchiae', 'branchiate', 'abranchiate'] 
['i', 'ai', 'lai', 'lain', 'latin', 'lation', 'elation', 'delation', 'dealation', 'dealbation'] 
['j', 'ju', 'jug', 'juga', 'jugal', 'jugale'] 
['k', 'ak', 'sak', 'sake', 'stake', 'strake', 'straked', 'streaked'] 
['l', 'la', 'lai', 'lain', 'latin', 'lation', 'elation', 'delation', 'dealation', 'dealbation'] 
['m', 'am', 'cam', 'camp', 'campo', 'campho', 'camphor', 'camphory', 'camphoryl', 'camphoroyl'] 
['n', 'an', 'lan', 'lain', 'latin', 'lation', 'elation', 'delation', 'dealation', 'dealbation'] 
['o', 'lo', 'loy', 'logy', 'ology', 'oology', 'noology', 'nosology', 'nostology', 'gnostology'] 
['p', 'pi', 'pig', 'prig', 'sprig', 'spring', 'springy', 'springly', 'sparingly', 'sparringly'] 
['q'] 
['r', 'ra', 'rah', 'rach', 'brach', 'branch', 'branchi', 'branchia', 'branchiae', 'branchiate', 'abranchiate'] 
['s', 'si', 'sig', 'spig', 'sprig', 'spring', 'springy', 'springly', 'sparingly', 'sparringly'] 
['t', 'ut', 'gut', 'gutt', 'gutte', 'guttle', 'guttule', 'guttulae', 'guttulate', 'eguttulate'] 
['u', 'ut', 'gut', 'gutt', 'gutte', 'guttle', 'guttule', 'guttulae', 'guttulate', 'eguttulate'] 
['v', 'vu', 'vum', 'ovum'] 
['w', 'ow', 'low', 'alow', 'allow', 'hallow', 'shallow', 'shallowy', 'shallowly'] 
['x', 'ox', 'cox', 'coxa', 'coxal', 'coaxal', 'coaxial', 'conaxial'] 
['y', 'ly', 'loy', 'logy', 'ology', 'oology', 'noology', 'nosology', 'nostology', 'gnostology'] 
['z', 'za', 'zar', 'izar', 'izard', 'izzard', 'gizzard'] 

Edit: Compte tenu de la mesure dans laquelle les branches fusionnent vers la fin, je pensais que ce serait intéressant de dessiner un graphique pour démontrer ceci:

Une extension intéressante de ce défi: Il est probable qu'il y ait plusieurs mots finaux d'équilibre pour certaines lettres.Quel ensemble de chaînes minimise le nombre de nœuds finaux (par exemple, fusionne le plus de lettres)?